Informationen zum Seminar: Die Wiener-Chaos-Zerlegung und (nicht-) zentrale Grenzwertsätze (SS 2025)

Zeit/Ort: 18.7.-20.7. als Blockseminar im Hebelhof (Feldberg) im Schwarzwald.

Vorbesprechung: Do, 30.1.25, 14:00 Uhr in Raum 232

Sprache: Vorträge/Teilnahme auf Deutsch oder auf Englisch möglich

Aktuelles

Voranmeldung per Email erwünscht an Gabriele Bellerino. Bitte geben Sie dann auch Ihre Vorkenntnisse in Stochastik an.

Inhalt

Wohingegen lineare Transformationen von Gaußprozessen ihre gaußsche Eigenschaft bewahren, gilt dies für nichtlineare Funktionale, beispielsweise additive Funktionale der Form

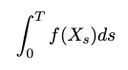oder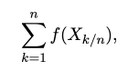

im Allgemeinen nicht. Die Wiener-Chaos-Zerlegung bietet einen Rahmen zur Analyse nichtlinearer Funktionale von Gaußprozessen. Es handelt sich hierbei um eine orthogonale Zerlegung

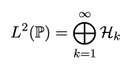
des Raumes der bezüglich P quadratintegrierbaren Zufallsvariablen, wobei P ein gaußsches Wahrscheinlichkeitsmaß ist. Dieses Konzept verallgemeinert dabei die Eigenschaften orthogonaler Polynome bezüglich eines Wahrscheinlichkeitsmaßes auf der reellen Achse auf ein (potentiell) unendlichdimensionales Szenario. Es stellt sich heraus, dass Elemente eines Wiener-Chaos 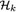als mehrfache Wiener-Itô-Integrale dargestellt werden können, welche wiederum gut verstandene Objekte sind.

In diesem Seminar werden wir die grundlegenden Eigenschaften des Wiener-Chaos untersuchen, beginnend mit der Hermite-Polynombasis. Anschließend wenden wir uns fortgeschrittenen Themen wie Anwendungen im Malliavin-Kalkül zu, einem unendlichdimensionalen Differential-Kalkül auf gaußschen Wahrscheinlichkeitsräumen (stochastische Variationsrechnung). Des Weiteren werden zentrale und nichtzentrale Grenzwertsätze für nichtlineare Funktionale von gaußschen und nicht-gaußschen Prozessen sowie Invarianzprinzipien behandelt.

Liste mit Vortragsthemen

folgt.

Literatur

Bücher

H.H. Kuo, Introduction to stochastic integration, Springer Verlag, 2006.
G. Peccati and M. S. Taqqu, Wiener chaos: moments, cumulants and diagrams, Springer Verlag, 2011.

Artikel

D. Nualart and G. Peccati, Central limit theorems for sequences of multiple stochastic integrals, The Annals of Probability 33(1), 2005
I. Nourdin and G. Peccati, Noncentral convergence of multiple integrals, The Annals of Probability 37(4), 2009
I. Nourdin, G. Peccati, G. Reinert, Invariance principles for homogeneous sums: Universality of Gaussian Wiener chaos, The Annals of Probability 38(5), 2010
H. C. Ho and T. Hsing, On the asymptotic expansion of the empirical process of long-memory moving averages, The Annals of Statistics 24(3), 1996
H. C. Ho and T. Hsing, Limit theorems for functionals of moving averages, The Annals of Probability 25(4), 1997
C. Döbler and G. Peccati, Quantitative De Jong Theorems in any dimension, Electronic Journal of Probability 22(2), 2017
M. A. Arcones, Limit Theorems for Nonlinear Functionals of a Stationary Gaussian Sequence of Vectors, The Annals of Probability 22(4), 1994
G. C. Rota and T. Wallstrom, Stochastic integrals: a combinatorial approach, The Annals of Probability 25(3), 1997
Y. Hu and D. Nualart, Renormalized self-intersection local time for fractional Brownian motion, The Annals of Probability 33(3), 2005
I. Nourdin and G. Peccati, Stein’s method and exact Berry–Esseen asymptotics for functionals of Gaussian fields, The Annals of Probability 37(6), 2009

Notwendige Vorkenntnisse

Notwendige Vorkenntnisse bestehen nur aus Kenntnissen der Wahrscheinlichkeitstheorie I. Für einige Vorträge sind Vorkenntnisse der Wahrscheinlichkeitstheorie II (Stochastische Prozesse) nützlich. Ihre individuellen Vorkenntnisse können bei der Vergabe der Themen jedoch selbstverständlich berücksichtigt werden.

Verwendbarkeit

Wahlmodul im Optionsbereich (2HfB21)
Mathematisches Seminar (BSc21)
Wahlpflichtmodul Mathematik (BSc21)
Mathematische Ergänzung (MEd18)
Mathematisches Seminar (MSc14)
Wahlmodul (MSc14)
Mathematisches Seminar (MScData24)
Elective in Data (MScData24)

Sprechstunden

Sprechstunde Dozent: Di, 16-17 Uhr
Sprechstunde Assistent: